Mortgage calculator algorithm - Andy Blog

Introduction

A mortgage calculator aims to simplify real estate investment. A good calculator enables us to determine loan amounts, mortgage qualification, affordability or whether we should be renting or buying.

The major variables in a mortgage calculation include loan principal, balance, periodic compound interest rate, number of payments per year, total number of payments and the regular payment amount. More advanced calculators can take into account other costs associated with a mortgage, such as taxes, maintenance fees and insurance.

This article describe common algorithms how to calculate mortgage payments.

Monthly payment formula for fixed rate(固定利率)

The fixed monthly payment for a fixed rate mortgage is the amount paid by the borrower every month. Typically, the payments ensure that the loan is paid off in full with interest at the end of its term. The monthly payment c is based on the annuity formula and depends upon:

r - the monthly interest rate, expressed as a decimal, not a percentage. Since the quoted yearly percentage rate is not a compounded rate, the monthly percentage rate is simply the yearly percentage rate divided by 12. e.g. if we got 3% annual interest of mortgage, r will be 3/12/100 = 0.0025
N - the number of monthly payments, called the loan’s term. e.g. if we apply 25 years term, N will be 12*25= 300 months
P - the amount borrowed, known as the loan’s principal.

In the standardized calculations used in the United States & Canada, c is given by the formula:

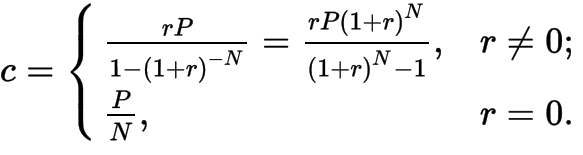
Process of derivation (推导过程)

The following derivation of this formula illustrates how fixed-rate mortgage loans work. The amount owed on the loan at the end of every month equals the amount owed from the previous month, plus the interest on this amount, minus the fixed amount paid every month. This fact results in the debt schedule:

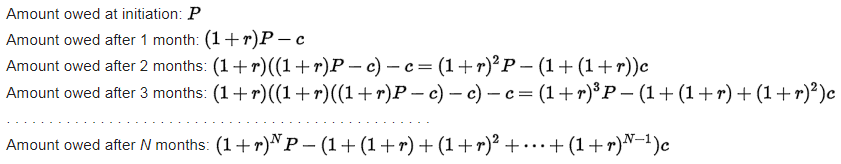
Here, we got a polynomial 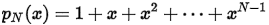if we suppose x = 1 + r. Please be advised that in mathematics, we have a simple closed-form expression for this formula - 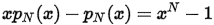. Therefore, Therefore, solving for this polynomial yields the much simpler closed-form expression:

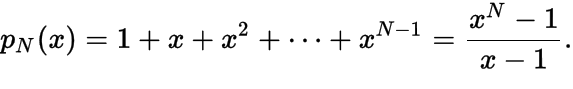
Replace x=1+r and we got amount owed at end of month N:

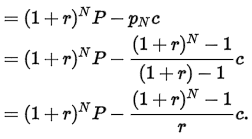
With a fixed rate mortgage, the borrower agrees to pay off the loan completely at the end of the loan’s term, so the amount owed at month N must be zero. For this to happen, the monthly payment c can be obtained from the previous equation to obtain:

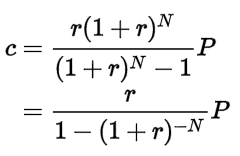
This is the formula originally provided. This derivation illustrates three key components of fixed-rate loans:

(1) the fixed monthly payment depends upon the amount borrowed, the interest rate, and the length of time over which the loan is repaid;
(2) the amount owed every month equals the amount owed from the previous month plus interest on that amount, minus the fixed monthly payment;
(3) the fixed monthly payment is chosen so that the loan is paid off in full with interest at the end of its term and no more money is owed.

Calculation example

For example, for a home loan of $200,000 with a fixed yearly interest rate of 6.5% for 30 years.

The principal is P=200000
the monthly interest rate is r=(6.5/12)/100}
the number of monthly payments is N=30 * 12=360

the fixed monthly payment equals $1,264.14 by previous formula.

  PMT(6.5 / 100 / 12, 30 * 12, 200000)
  = ((6.5 / 100 / 12) * 200000) / (1 - ((1 + (6.5 / 100 / 12)) ^ (-30 * 12)))
  = 1264.14

Total Interest Paid formula for fixed rate

The Total Interest Paid (I) tells us how much interest you will pay over the lifetime of the mortgage loan. It is the difference of the total payment amount (c * N) and the loan principal (P): The calculation assumes we you will make all payments as scheduled.

I = c * N - P

c is the fixed monthly payment
N is the number of payments(number of months) that will be made
P is the initial principal balance on the loan

Calculation example

For example, for a home loan of $200,000 with a fixed yearly interest rate of 6.5% for 30 years, we already calculated that monthly payment is $1264.14.

I = 1264.14 * 30 * 12 - 200000 = 255090.4

In this example, Total Interest Paid accounts for 120 percent of the value of original loan.

Cumulative Interest Paid formula for fixed rate

Moving forward, the cumulative interest paid at the end of any period N can be calculated by:

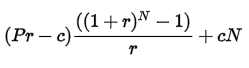
P is the initial principal balance on the loan
r is the monthly interest rate
c is the fixed monthly payment
N is the number of payments(number of months) that will be made

Calculation example

For example, for a home loan of $200,000 with a fixed yearly interest rate of 6.5% for 30 years, we already calculated that monthly payment is $1264.14.

After one year (12 months) payment, the interest we already paid is:

(200000 * 0.065/12-1264.14) * ((POWER(1+0.065/12,0)-1)/(0.065/12))+1264.14*0
= 12934.18

Remaining loan balance formula for fixed rate

Here is the formula to calculate the remaining load balance (B) of a fixed payment load after p months.

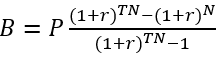
P is the initial principal balance on the loan
r is the monthly interest rate
TN is the total months of payments (load term)
N is the number of payments(number of months) that will be made

Calculation example

For example, for a home loan of $200,000 with a fixed yearly interest rate of 6.5% for 30 years, we already calculated that monthly payment is $1264.14.

After one year (12 months) payment, the interest we already paid is:

200000*(POWER(1+0.065/12, 30*12)-POWER(1+0.065/12, 1*12))/(POWER(1+0.065/12, 30*12)-1)
= 197764.5491

Calculations for adjustable rate(浮动利率)

While adjustable-rate mortgages are more complicated as did the calculations involved. Lending became much more creative which complicated the calculations. Subprime lending and creative loans such as the “pick a payment”, “pay option”, and “hybrid” loans brought on new era of mortgage calculations. The more creative adjustable mortgages meant some changes in the calculations to specifically handle these complicated loans.

To calculate the annual percentage rates (APR) many more variables needed to be added, including:

the starting interest rate;
the length of time at that rate;
the recast;
the payment change;
the index;
the margins;
the periodic interest change cap;
the payment cap;
lifetime cap;
the negative amortization cap;
and others.

Most lenders created their own software programs and even had contracted special calculators to be made by Calculated Industries specifically for their mortgage calculations. There is not a perfect formula to make calculations for adjustable rate mortgage.